Even if he does find gold, he has to get past the robbers that are targeting prospectors. The thieves have been very productive in Colorado so Bob only has a 55% chance of eluding them. However, the California thieves prefer to surf which gives Bob an 85% chance of not being robbed. If he manages to make it to the appraisal office, the appraisal can differ tremendously from appraiser to appraiser. In Colorado, a high appraisal is $350/oz and a low appraisal is $125/oz. California’s appraisers are more generous in that their high appraisal is $400/oz and the low is $240/oz.

Finally, because of budget cutbacks in both states, there aren’t enough revenue agents to collect taxes on gold. California’s tax on gold is 14% but their agents are paid well so there is a 75% chance that Bob will have to pay the tax. On the other hand, Colorado’s tax is 23% but its agents prefer to ski, so there is only a 60% chance of paying the tax.

a) What should Bob do if he is risk neutral? Create a decision tree to determine the expected value of the gold find from California and Colorado.

ANSWER

Below is the decision tree for this problem. If Bob cannot find gold, he still has to bear the cost of the operation. If the gold is stolen en route to the appraisal office, then he still has to pay the mining costs. If Bob makes it to the appraisal office then his gold may be appraised at either the high or low value and taxes may or may not be levied. The values at the end of the tree branches are calculated like the following example:

High Colorado appraisal, taxed = 2000 oz. x $350/oz x (1-23%) - $50,000 = $489,000

The $50,000 must be included to account for the cost of mining the gold.

Working back through the tree we find that the expected value for Colorado is $20,922 which is much higher than the expected value for California ($-20,121). Based on these values, Bob should mine for gold in Colorado.

(Sorry! The Decision Tree did not convert to HTM)

b) Bob thinks he can improve his chances in California by purchasing special equipment for California’s geology. Bob’s believes that he can purchase this equipment for $50,000 and that his probability of finding gold will increase to 50%. Should Bob buy the equipment?

ANSWER

Absolutely. The cost of the equipment will reduce the value of the gold (at the end of the tree branches) by $50,000 for California. Working back through the tree, one can calculate that the new expected value for the state of California will increase to $38,508. As this is higher than the expected value for Colorado ($20,922), Bob should purchase the new equipment and mine for gold in California.

2. A. Solvay Engineered Polymers (SEP) is a plastic supplier for the automotive industry. Currently, they are producing at capacity and are interested in building an additional line. The new line will have the capacity to produce 40 million pounds of plastic in one year. The cost to produce this line will be 30 million dollars. The SEP marketing team predicts that there is a 40% chance of producing at 100% of capacity, 25% chance of at 50% capacity, and a 35% chance of not needing the additional line. Assuming the plastic will sell for a net profit of $1.00 a pound, what is the expected value after the first year of sales?

B. Suppose instead there was a 5% chance of producing at 100% capacity, 10% chance of producing at 50%, 40% chance of producing at 25%, and a 45% chance of not needing the additional line. What would the new expected value be?

C. How many years would it take for SEP to break even, given the probabilities in part B?

D. Assuming the probabilities in part A, create a decision tree if the probability of selling the material for given prices are as follows:

3.  Papa of Papa’s Pizza is considering whether to offer a new sandwich, the pizza pocket hot sub, in his shop that is located in a local college town.

Papa believes he has the possibility of the following revenues with the associate probability of each level of revenue occurring:

1. What is the expected profit value? (Show the E(v) using the formula and a decision tree to display the values)

E(v) = p₁v₁ + p₂v_{2 +} p₃v₃
 

E(v) = .15 (2500) + .5 (6000) + .35 (15000)

 

E(v) = $8,625

 

 
2. Based on the expected profit, which alternative would be chosen?

 

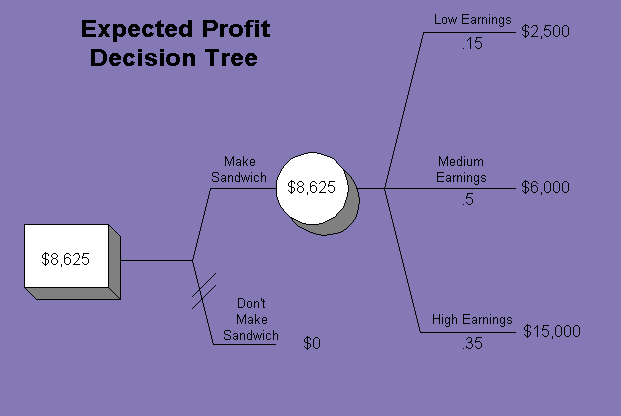
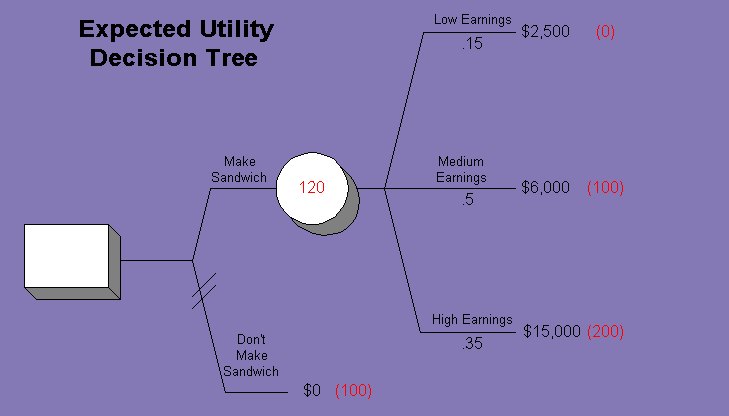
Since the expected value instructs a decision maker to choose the course of action that generated the greatest expected profit, Papa would choose to make the pizza pockets with an expected value of $8,625 verse choosing to not make the pizza pockets with an expected value of $0.

 

Papa’s Pizza is a small business with limited capital. The risk of the investment must be looked at. The utilities for the different outcomes are:

 

Low Earnings U(2500) = 0

Medium Earnings U(6000) = 100

High Earnings U(15000) = 200

 

3. Using these utility values, how does Papa’s Pizza evaluate the option to expand their menu to include the pizza pocket hot subs?

 

Papa’s Pizza will need to look at the expected utility of expanding their menu.

 

E(U_expanding) = .15 U(2500) + .5 U(6000) + .35 U(15000)

 

E(U_expanding) = .15 (0) + .5 (100) + .35 (200)

 

E(U_expanding) = 120

 

4. Suppose the indifference probability is equal to 1/3, therefore Papa’s Pizza is indifferent between a certain $0 of not offering pizza pockets and a

1/3 – 1/3 – 1/3 risk of offering pizza pockets. What is the expected utility U(0) of not expanding the menu to include the pizza pocket hot subs?

 

The expected utility of the 1/3 – 1/3 – 1/3 gamble is:

 

1/3 U(2500) + 1/3 U(6000) + 1/3 U(15000)

 

1/3 (0) + 1/3 (100) + 1/3 (200) = 100

 

Since Papa’s Pizza is indifferent between the option of a certain $0 and the
1/3 – 1/3 – 1/3 gamble the two alternatives must have the same utility. Therefore the U(0) = 100.

5. What decision should Papa’s pizza make using the expected utility information (show the decision process on a decision tree).