
1. Lima Locomotive Works produces locomotives for the North American market. The product life cycle is 4 years. The long run cost is $1,000,000 per unit.
a. Assume costs and demand remain unchanged over the productís life. Demand for each two year period is represented by P=1.5x106- 500Q. To maximize profits, what is the price and quantity of units sold over the product life? What is the total profit?
Apply MR=MC R=PQ
P=Q/R
R/Q=1.5x106-500Q
R=1.5x106Q-500Q2
dR/dQ=1.5x106-1000Q
1.5x106-1000Q=1x106
Q=500 for each period
Qtotal=500x2=1000
P=1.5x106-500(500)
Total quantity produced 1000.
Unit price $1,250,000.
Total profit $250 million.
b. Suppose Lima Locomotive Works can lower costs based on experience gained during initial production. Lima now divides the product life into two periods, the first two years and the remaining eight years. For the first period the unit cost is the same as above. For the second period, the unit cost is c2=2x106 - 1750Q1. What output quantities, Q1 and Q2, should Lima set in each period? What is the total profit
?
Apply MR=MC for the second period
1.5x106-1000Q2=2x106-1750Q1
Solve for Q2
Q2=1.75Q1-500
Substitute Q2 into the price equation
P2=1.5x106-500(1.75Q1-500)
P2=1.5x106-875Q1+.25x106=1.75x106-875Q1
Determine second period profit
p2=(P2-c2)Q2
p
2=[(1.75x106-875Q1)-(2x106-1750Q1)]Q2p
2=(875Q1-.25x106)(1.75Q1-500)= 1531.25Q12-.875x106Q1+1.25x106Maximize total profit
p
= p1+ p2=[(1.5x106-500Q1)Q1-1x106Q1]+ 1531.25Q12-.875x106Q1+1.25x106d p/dQ1=1.5x106-1000Q1-1x106 +1531.25Q1-.875x106=0
d p/dQ1=531.25Q1-.375x106
Q1=705.88=706
P1=$1,147,000
Q2=735.5
P2=$1,132,250
C2=2x106-1750Q1=764,500
Period 1 quantity produced 706.
Period 2 quantity produced 736.
Total profit $374 million.
2. Samís Super Heaters assembles 2 portable ceramic heaters in the same location. The total fixed costs for the company are $90,000. The products have the following characteristics:
|
|
PRODUCT |
|
|
|
A |
B |
|
Average Variable Costs (AVC) |
$15.00 |
$20.00 |
|
Current Price (P) |
$18.50 |
$25.00 |
|
Quantity Sold (Q) |
15,000 |
10,000 |
a. What is the profit for the company?
p
= (TRA - VCA) + (TRB - VCB) - FC= [(18.50 * 15000) - (15000 * 15)] + [(25.00 * 10000) - (10000 * 20.00)] -90000
= (277500 - 225000) + (250000 - 200000) - 90000
= 52500 + 50000 - 90000
p
= $12,000
b. Should the company stay in business?
Yes, because PA > AVCA (18.50 > 15.00) and PB > AVCB (25.00 > 20.00) and the profit is positive.
Suppose the price of product B falls to $22.00 and quantity sold of product B increases to 15,000 units.
c. Should the company stay in business in the short run?
Yes, because PA > AVCA (18.50 > 15.00) and PB > AVCB (22.00 > 20.00).
d. Should the company stay in business in the long run?
No, because although the PA > AVCA and PB > AVCB the positive contribution that they make toward covering the fixed costs are not adequate and the profit is not positive.
p
= (TRA - VCA) + (TRB - VCB) - FC= [(18.50 * 15000) - (15000 * 15)] + [(22.00 * 15000) - (15000 * 20.00)] -90000
= (277500 - 225000) + (330000 - 300000) - 90000
= 52500 + 30000 - 90000
p
= - $7,500
Suppose the price of product A increases to $19.00 and the quantity sold stays the same but the price of product B falls to $19.50 and quantity sold of product B increases to 20,000 units.
e. Should the company continue to produce both products in the short run?
No. The production of product B should cease immediately because PB < AVCB, but the production of product A should continue in the short run.
f. Should the company continue to produce product A in the long run?
No. The profit with no production of B and only the slight increase in profit from product will cause a larger loss of profit.
p
= (TRA - VCA) + (TRB - VCB) - FC= [(19.00 * 15000) - (15000 * 15)] + [(19.50 * 0) - (0 * 20.00)] -90000
= (285000 - 225000) + 0 - 90000
= 60000 - 90000
p
= - $30,000
3. Solvay Engineered Polymers (SEP) is one of the leading Polypropylene (PP) producers in North America. SEP sells their commodity material to various injection molders who then produce a variety of finished goods, ranging from childrenís toys to plastic patio chairs. SEP has the capacity to produce 400,000 lb. of PP every day. The average total cost to produce 1,000 lb. (1 gaylord) of material is $400 and they can sell the gaylord for $750. SEP also sells its PP to customer compounders, who mix it with other materials to produce Thermo Plastic Olefins (TPO) used mainly for exterior automotive parts.
After 20 years in the PP business, SEP decides that it wants to investigate entering the TPO business. After much research, they find out that TPO is made by combining 80% PP, 15% elastomer, and 5% mineral filler. The bean counters determine the average cost of producing a gaylord of TPO is $250 excluding the price of the PP (assuming the $250 cost is variable and the average total cost is constant at all outputs of volume). The gaylord of material can be sold for $800. The maximum capacity of TPO per day is 250,000 pounds.
a. Should SEP Produce TPO? Is it profitable?

b. Suppose that the demand for PP decreases until the most profitable quantity of production is $300,000. What should SEPís production strategy be?
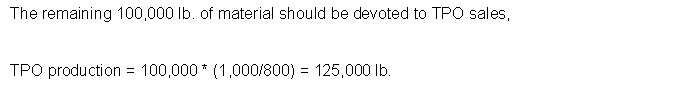
c. Suppose SEP found a way to make TPO profitable enough to put the product into production. Employees are hired and machinery is purchased. In order for SEP to produce TPO at capacity (250,000 lb. per day), 50 hours of labor is required. The average wage rate per employee is $10 per hour, and other variable costs (materials, machinery, rent, etc.) average $8 per gaylord. The marketing group estimates the demand of TPO to be P = 120 - 2Q, where P is the price per gaylord and Q is the daily demand.
How many additional gaylords can be produced by an extra hour of labor? What is the marginal cost (MC) of an additional gaylord? In order to maximize profit, what price and output should the firm sell at? Is the production capacity fully utilized? What contributions does this production line have?
