1. Two firms compete by selling popular brands of soft drinks in the
same market. The payoff table below represents the quantity
combinations and their associated payoffs for the two firms. Study the
table and answer the following questions.
Firm 2's Quantity (000's)
5 28,28 40,20 52,20
Firm 1's Quantity (000's)10 20,40 36,36 52,40
15 20,52 40,52 60,60
a. Does either firm have a dominant strategy?
No
b. If Firm 1 chooses to produce 10,000, what is Firm 2's response?
If Firm 1 chooses to produce 15,000, what is Firm 2's response?
c. What are the equilibrium quantities?
15,15
2. Consider two duopolistic companies competing in a market of constant
size. Find the companies' equilibrium strategies.
B1 B2 B3
A1 8 9 -6
A A2 -5 -8 -7
A3 6 7 5
(A3,B3). Note that this is also the maximin strategy.
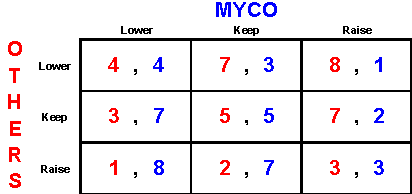
3. At MYCO Dice Company, we manufacture the worldís highest quality dice for for non-professional use. We are one of a few companies that dominate the industry with over 75% of the market share held between 4 companies (Oligopoly). All other competitors combined make up the other 25% of the market.
We have been building our product for many years, and continue to find ways to improve our manufacturing process to lower cost and increase profits. Our main competitors (OTHERS) have been working hard on reducing their costs in similar ways. With a relatively steady demand for our product, it is necessary to continually re-evaluate our pricing strategy to maximize profits.
Over the years, we have been tracking the changes in both our own and our competitors cost and demand curves in order to maintain an "edge" over the competition. We take that information and develop pricing-strategy models that are used to determine what (if any) price changes should be made.
In this report, the latest pricing model is provided. It is considered to be valid for the next 6 months. Using this model we need to analyze the "state" of the current market and develop a "favorable" pricing strategy for the next 6 months.
On the next page, is the pricing model. Apply each of the following questions to the model and try to draw conclusions.
Raising or lowering the price is assumed to be 20% in this model. The numbers in each of the "Cells" indicate the relative impact on "TOTAL PROFITS" experienced by the company(ies) on the corresponding axis. The numbers shown in
"blue" represent MYCO.
Known market conditions:
Constant Demand
Stable Product
Steady Economy
No New Technology
Below is the scale used in the model:
RELATIVE SCALE
1 = Very Large Decrease In Profits
2
3
4
5 = No Change In Profits
6
7
8
9 = Very Large Increase In Profits

ANALYSIS
INITIAL OBSERVATIONS:
The appearance of the chart looks like that of a zero-sum game if both groups choose different strategies. However, if both groups choose the same strategy, the impact on them is the same.
IS THERE A DOMINANT STRATEGY?
Yes, the dominant strategy (as well as our competitors) is to lower prices.
IS THERE "NASH" EQUILIBRIUM?
Yes, the cell in position (Lower, Lower)
WHAT WOULD BE OUR "MAXI-MIN" STRATEGY?
There is really no valid Maxi-Min Strategy Here.
THAT WOULD OUR "ITERATED DOMINANCE" STRATEGY BE?
Again, this strategy would lead both groups to lower their prices.
CONCLUSION
While it is best for both groups to maintain their current prices, it is unlikely to happen in the long-run without some type of binding agreement (This would be Illegal). It would always be tempting to lower prices to try and obtain additional profits. Once either side deviates, both groups will settle down to lower their prices, which will ultimately lower their profits.
When considering this example, it would appear as if MYCO is not operating as an Oligopolist, but rather as a pure competitor. The prices of the product will tend to keep going lower and lower until either MYCO or the competition hits their average cost limit. At this time, there is likely to be exit from the market resulting in the need to reevaluate strategies.
The best strategy for MYCO is not to change their prices unless prompted to do so by the competition and make sure that their average cost of producing stays below the average for the industry.
4. The executives at one automotive company (C) are in a quandary. One competitor (B) recently announced that it was going to offer side airbags (SAB) on most of its models within the next year. The Sales and Marketing (S&M?) area is concerned that company B will develop a significant competitive advantage as a result. Despite its best efforts in advertising and other promotions, Sales & Marketing estimates 25,000 customers per year will be lost to company B as a result of A not having SAB. Each customer represents an average of $1,000 profit for the company.
Engineering has identified two proposals for implementing side airbags. (P1 & P2) Engineering estimate proposal P1 (existing methodology) will cost $50 million and take 1 years to implement. P2 (a new methodology) is estimated to cost $10 million but will require 2 years to implement. The new technology is technically superior (and obviously so to the customer) to the existing technology, however it is still in development at company B and therefore requires the extra year. The two technologies are so very different that the costs of doing both (P3=P1+P2) yield additional "congestion" costs of $20 million.
Furthermore, it is unknown whether company B will introduce the existing or the new technology. P1ís effectiveness at stopping the migration of customers to B is severely diminished (-30%) if B introduces methodology B. In light of the best information available, Company C must decide whether it should respond by also adding SAB to its products, and if so, which methodology(s) to use.
Analysis:
Construct a payoff table to show the possible results.
|
Company Bís Methodology (Cumulative 3 years) |
|||
|
Methodology 1 |
Methodology 2 |
Future Prospects for Company C |
|
|
Do Nothing |
-$25 million (x3) |
-$25 million (x3) |
Continuing loss of perhaps greater proportions |
|
-$75 million |
-$75 million |
||
|
Proposal 1 |
-$25 million (x1) -$50 million |
-$25 million (x1) -$7.5 million x 2 -$50 million |
Continuing loss possible if Methodology 2 is offered by Company B |
|
-$75 million |
-$90 million |
||
|
Proposal 2 |
-$25 million (x2) -$10 million +$7.5 million (x1) |
-$25 million (x2) -$10 million |
Competitive advantage may be achieved in Methodology 1 is offered by Company B. |
|
-$27.5 million |
-$35 million |
||
|
Proposal 3 (1+2) |
-$25 million (x1) -$50 million -$10 million -$20 million +$7.5 million |
-$25 million (x1) -$50 million -$10 million -$20 million |
Competitive advantage may be achieved in Methodology 1 is offered by Company B. |
|
-$97.5 million |
-$105 million |
||
Identify Company Cís dominant strategy (if one exists).
Clearly, proposal 2 becomes Cís dominant strategy. Regardless of Bís methodology, proposal 2 minimizes the cumulative 3-year losses and eliminates all long-term risk (the risk of B choosing Methodology 2 and its consequences).
How might the analysis be different if:
Marketing and Sales underestimated the number of customers this new safety item would attract?
As the prediction of the number of customers "stolen" increases, the value of Proposal 1 increases and becomes more favorable. At some point (95,000 defections), it will become profitable to utilize Proposal 3 (1+2).
The average profit per customer changes?
If the economy is expected to be good in the next 2-3 years, the average profit per customer may increase. This can make it more attractive to favor Proposal 1.
The diminishing effects of Methodology 2 is less than predicted? More?
Changes in the effectiveness of methodology 2 over 1 can greatly affect the "payback". If the rate of customer defection to the newer technology is small, the payback period becomes longer making proposal 2 less favorable. However, if the defection rate is large enough, proposal 2 becomes more favorable.
What happens to the analysis if Proposal 2 gets delayed by a year?
A new payoff table would need to be constructed to determine the results.
Is the game a zero-sum or non-zero-sum game?
The problem is assumed to be a zero-sum game. Company Cís loss is company Bís gain.
Does company Cís strategy change if it know with certainty what company Bís plans to do?
No. Given the best available data, it is always in company Cís best interest to at least pursue Proposal B. The only way for Bís strategy to affect Cís best decision is if it delays introducing SABís for a year (or longer).
Conclusion:
As the variables used in making a decision change, the best course of action can also change. Be prepared to periodically review decisions and react if conditions have changed significantly enough to warrant change.