1. The average variable cost for the production of an automotive part is given by
AVC = 1,000,000 - 1,000Q + 0.3Q2
- Determine the firm's short run supply equation
.
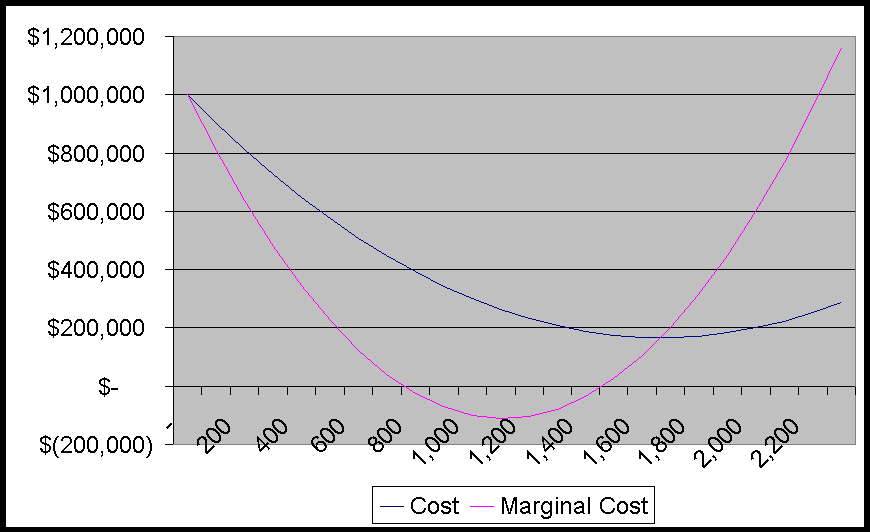
b. Determine the minimum possible price for the firm in the short run.
The short run supply curve is MC above the minimum point of the AVC.
Marginal cost is the derivative of the total variable cost.
Thus,
VC = (AVC) * Q = 1,000,000Q - 1,000Q2 + 0.3Q3
MC = 1,000,000 - 2,000Q + 0.9Q2
The shut down point is the minimum point of AVC.
The derivative of AVC is
dAVC/dQ
= -1000 + 0.6Q
Setting this equal to zero, yields Q = 1,667
The shut down price is equal to the AVC at Q = 1,667.
AVC = 1,000,000 - 1,000(1,667) + 0.3(1,667)2
= 1,000,000 - 1,667,000 + 833,333
= $166,667
2. A firm enters a new market with a new product and decides to price this product at $50 each. The Firm’s cost function is C=288+6Q+2Q2.
a. What is this firm’s profit maximizing quantity?
To find the profit maximizing quantity, set MR=MC
R=PxQ or 50Q and MR=dR/dQ=50
MC=dC/dQ=6+4Q
setting MR=MC yields 50=6+4Q and Q=11
b. In the long run (assuming perfect competition), what will be the equilibrium price and quantity?
In the long run, P=MR=MC=minAC so set MC=minAC
AC = C/Q or (288+6Q+2Q2)/Q and MC=6+4Q
solve for Q=12
To find P, set P=MC or P=6+4Q solve to find P=$54
c. What is the firm’s supply curve?
The supply curve is found by setting P=MC or P=6+4Qf. Rearrange to get Qf=.25P-1.5
d. If the market demand function is Qd=2500-10P, what will be the market demand for this product?
We know that the long-run equilibrium price is $54. Substitute this value into the market demand function to find the demand quantity.
Qd=2500-10x54=1960 units
e. How many firms will supply this market (assume they all have similar cost functions)?
The number of firms is equal to the total demand divided by the quantity each firm will produce. N=Qd/Qf=1960/12=163.33 or approximately 163 firms
f. What is the market supply function?
The market supply function is the number of firms times the individual firms’ supply function. Qs=163Qf=163(.25P-1.5) or Qs=40.75P-244.5
3. JW Industries is a small firm in a competitive market with many other small firms. The industry’s supply and demand curves are (see graph below):
 P = 500 + 2Qs
P = 500 + 2Qs
P = 1000 - .5Qd
a. Find the market’s equilibrium price and output.
Set the two equations equal to each other:
500 + 2Qs = 1000 - .5Qd
2.5 Q = 500
Q = 200 units
Plug this value of Q into either equation to get the equilibrium price
500 + 2(200) = $900
By inspection, we see that our calculated answers match the intersection point (equilibrium point) of the two curves on the graph above.
- Now suppose Uncle Sam decides they are going to pay for every American to have a copy of the Jerry Springer outtakes tape by imposing a $29.95 tax on every unit sold by all companies in JW’s industry. What happens to the industry supply curve? Find out the new competitive price and output. Finally, what portion of the tax has been passed on directly to consumers?
The supply curve will have a parallel upward shift.
The new tax means the supply curve has a new formula that is increased by $29.95.
Old formula for supply was P = 500 + 2Qs
Therefore the new formula is:
P = 529.95 + 2Qs
Now we find the new competitive output by setting the new formula equal to the existing demand curve:
529.95 + 2Qs = 1000 - .5Qd
2.5 Q = 470.05
Q = 188 units (instead of 200)
Plug this new value of Q into either equation to get the equilibrium price
529.95 + 2(188) = $905.95 (instead of $900)
This indicates $5.95 or about 20% of the tax increase have been passed onto the consumer. Note that the price the producers receive net of tax is:
$905.95 - $29.95 = $876
- Now suppose the government decides to directly tax the consumer the $29.95 to cover the costs of the tape. What is the effect on the industry demand curve? Find the new competitive price and output. Compare your answer to question 2.
In this case the demand curve will have a parallel downward shift.
The direct tax means the demand curve has a new formula that is decreased by $29.95.
Old formula for demand was P = 1000 - 0.5Qd
Therefore the new formula is:
P = 970.05 – 0.5Qd
Now we find the new competitive output by setting the new formula equal to the existing supply curve:
500 + 2Qs = 970.05 – 0.5Qd
2.5 Q = 470.05
Q = 188 units (instead of 200)
Plug this new value of Q into either equation to get the equilibrium price
500 + 2(188) = $876 (instead of $900)
$876 is the price before tax. Price after tax is $876 + $29.95 = $905.95
Note these values are identical to those in part b. Therefore it does not matter if the tax is passed onto the consumers or the suppliers.
.
- The monthly supply and demand curves for comic books in a competitive market are:
Qd= 150-15P and Qs = 87+3P where Q is in 1000s
- Find the competitive price, output and revenue to the sellers.
Qs = Qd
87+3P = 150-15P
18P = 63
P= $3.50
Q = 97.5 => 97 comic books
Revenue = P*Q = $3.50*97 = $339.50 in $1000s
- Suppose the supply of product increases by 15% (i.e., both slope and intercept terms increase by 15%). Determine the new optimal price, quantity and revenue.
Qs'= 100 + 3.45P
Thus, P'= $2.71, Q'=109 (The increase in supply lowers P and raises Q.)
Revenue = P'*Q' = $2.60*111 = $295.4 (Note the drop in revenues--demand must be inelastic.)
- Is the supply elastic or inelastic at the new price?
Es = dQ/dP(P/Q) = 3.45(2.71/109) = 0.09 (Inelastic)
The Acme Company, one of the comic book suppliers, also sells framed pictures of comic books. Suppose the Acme Comic Company is operating in a perfectly competitive market for frames with a long-run total cost equation:
LTC = 45+3Q+2Q2
a. Determine the long run price and output
LAC=LMC
45/Q+3+2Q = 3+4Q
45+3Q+2Q2 = 3Q + 4Q2
45=2Q2
Q= 5
P=LAC=LMC= 3+4(5)
P=$23
- Suppose the Market demand curve is Q=300-4P. How many companies would exist long term?
Q=300-4(23)= 208
If long run output (from part a) is Q=5, then 208/5= 41.6 => 41 companies could exist.
- Suppose demand decreases and the market price drops to $20. Explain what will happen.
Firms will drop their output to 4 units (set P=LMC). However, they will now be losing money (P<LAC). Some firms will exit (decreasing supply) until price rises to $23.
5. A perfectly competitive market has the following demand and supply equations
QD = 200 – 10P
QS = 20P – 40
A typical firm has the short run total cost function
STC = 4 + Q2 - 2Q
- Determine the market equilibrium price and quantity
Set QD = Qs
200 – 10P = 20P – 40
30P = 240
P = 8
Setting this value in the demand equation the quantity is 200.
- Determine the typical firm's output and profit. How many firms are operating in the short run.
Set P = MC
8 = 2Q - 2
Q = 3
Profit = R-C
= (3)(8) – (4 + 9 - 6) = 17
No of firms in the short run are 120/3 =40
c. Suppose the government imposes a tax of $2 per unit of output on all firms in
the market? What effect does this have on the supply curve? Find
the competitive price and output. What portion of the tax has been passed on to consumers via a
higher price?
If a tax of $2 per unit is levied on suppliers. The industry supply curve
shifts upwards, increasing the price intercept by $2 implies
P = 4 + 0.05Q. Setting the market demand equal to the new supply equation
200 + 10P = 80 + 20P
200 + 80 = 30P
P = 9.33
Q = 106.7
Consumers pay the price of $9.33. $1.33 of the $2 tax increase (or 66.5%)
is passed on to the consumer. The price the producers receive (net of tax)
is $7.33.
d. Suppose a $2 sales tax is imposed on the consumers. What effect does this
- have on the demand curve? Find the new competitive price and output. Compare this answer to the findings in part c.
If tax of $2 is levied on the consumers, the demand curve undergoes a downward
shift and becomes P = 180 -10P. Setting the new demand curve equal to the
supply curve
180-10P =20P-40
P = 220/30 = 7.33
Q = 106.7
The price inclusive of taxis 7.33+2=9.33. The quantity results in part 3 and 4 are
the same. Whether a given tax is levied on suppliers or consumers makes
no difference in the ultimate competitive equilibrium.
e. If the prices of inputs increase and the new cost function of the typical firm is
4 + Q2 - 3Q what effect will it have on the short run supply curve? On market
supply and prices in the short run and in the long run?
Compute the new market and firm supply curve. Determine the new
equilibrium price and quantity. Compute the profits of the firm.
An increase in the variable cast will raise the firm’s short run marginal cost
and average cost curves. The short run supply curve will shift upwards.
Industry supply will also go up. The new intersection of the short run demand
and supply implies a higher short run price. The increase in minimum average
cost means a higher long-run price as well.
A firms supply curve is found by setting
P = MC
P = 2Q - 3
Q SF = P /2 - 3/2
The new market supply curve is (P /2 – 3/2)* 40, as the no of firms in the
short-run are 40
QS’ = 20P – 60
The new price is
QD = QS’
200-10P =20P-60
P = 260/30 = 8.66
Q = 200 – 86.6 = 113.4
Each firm will supply now a quantity of 2.83
As the variable cost increases in the short-run the price increases and
the quantity decreases.
Profit = (8.66)(2.83)-(4+8-8.49) =20.99
f. Determine the long run zero profit equilibrium using the new cost function. How
many firms serve the market?
Long run Equilibrium,
P = minAC
AC = 4/Q + Q - 3
MC = 2Q - 3
Qmin is obtained by setting AC=MC
4/Q + Q - 3 = 2Q - 3
Q2 = 4
Qmin = 2
minAC = P=1
In turn Q = 200 – 10 = 190
The No of firms is 190/2 = 95firms
As there are positive profits more firms will enter in the long run.
g. Suppose the typical firms total fixed cost increases what effect will it have on the
short run supply curve? On market supply and prices in the short run and
in the long run?
As long as the firm continues to earn a positive economic profit, an increase in
the firm’s fixed cost has no effect on the marginal cost, m supply, or price in the
short run. In the long run however, price must increase to cover the higher level
of minimum average cost.
6. T-shirts-R-us, a retailer of novelty T-shirts in Gatlinburg, The firm has the following information.
|
Total cost = 75+Q2 - 6Q
Average cost = 75/Q+Q-6
Marginal cost = d(75+Q2-6Q)dQ=2Q-6 |
a. What is the output that minimizes the firm’s average cost?
|
Set AC=MC
75/Q+Q-6=2Q-6
75/Q+Q=2Q
Q2=75
Q=8.66
MC=2(8.66)-6
MC= $11.32=AC |
b. What is the equation for the firm’s supply curve?
|
P=MC=2Q-6
P=2Q-6
Q=(P+6)/2 |
c. If industry demand is given by the equation Q=485-18P
- What is the long-run competitive price?
- What is the industry output at that price?
- How many firms will there be in the industry?
|
1. P=minimum AC=$11.32
- Q=485-18P=281,
3. N=281/8.66=32 |
d. If demand increases to Q=700-17P,
What is the new short-run industry price and output, i.e., before new firms enter the market?
|
N=32, Qf =(P+6)/2
Qs=32(P+6)/2
Qs=16P+96
Set supply = demand
16P+96=700-17P
P=18.30
Qs=16(18.30)+96
Qs=389 |
e. What is the firm’s optimal level of output at the new price?
|
Qf=(P+6)/2
Thus Q=12 at P=18.3 |
f. How many new firms will enter the market to take advantage of the economic profit to be made?
|
Qd=700-17P
P must return to the minimum AC.
Qd=700-17(11.32)=508
Thus N=508/8.66=59 total firms
59-32=27 new firms will eventually enter. |
6. After evading conviction on criminal charges (by shredding all damaging evidence), the dirty politician has decided to make and sell a better shredding machine. Of course, there are many similar politicians throughout the world, so competition is heavy. There is a good market for these machines; other dirty politicians and kids looking to destroy their report cards before mom and dad sees them. Given the market conditions, the following supply, demand and cost functions are given:
Qd = 180 – 5P
Qs = 25P – 30
STC = 10 + Q2 – 7Q
- Determine the market equilibrium price and quantity for shredding machines.
V
Set Qd = Qs
180-5P = 25P-30
210 = 30P
P = 7
V
Put the price into the demand equation:
Qd = 180-5(7)
Qd = 145
- Determine the output and revenue for the dirty politician
V
Set P = MC
7 = 2Q-7
14 = 2Q
Q = 7
V
Revenue = Price(Quantity)
R = 7(2)
R = 49
- Determine the number of dirty politicians that will be in the marketplace to provide shredding machines
V
The quantity demanded is 145 and the quantity supplied by a company at the price of 7 is 7. So…
# firms = 145/7
# firms = @21
- Now really stretch the imagination and suppose that there are some good politicians out there who wanted to penalize the dirty politicians. Given the effectiveness of the new shredding machines, a criminal conviction is out of the picture. Instead, the good politicians decide to impose a $3.00 tax on the dirty politicians who make the machines. What effect would this feeble attempt have on the supply curve?
®
The tax on the producers will shift the price intercept up by $3.00.
Qs = 25P-30
25P = Qs+30
P=.04Qs+1.2+3
P = .04Qs+4.2
- Compute the new price and output after the tax on the producers.
®
Take the price equation above and multiply both sides by 25 to re-establish the supply curve.
(25)P = 25(.04Qs+4.2)
Qs = 25P-105
®
Then set the new supply curve equal to the demand curve as above.
25P-105 = 180-5P
30P = 285
P = 9.5
®
Substitute the new price into the demand equation.
180-5(9.5) = Q
Q = 132.5
- Who pays for this tax?
®
Dirty politicians pay for this tax in its entirety. More specifically, the politicians who are buying the machines will pay most of it ($2.50) while the dirty politicians who make them pay only ($.50). That is until an industrial aid package could be voted into law. S

 P = 500 + 2Qs
P = 500 + 2Qs